Use Polar Coordinates Describe Level Curves

By Ra_Alison571 11 May, 2022 Post a Comment

Misner Thorne Wheeler - Gravitation. X is a girl Do our first leader.

11 4 Area And Arc Length In Polar Coordinates Mathematics Libretexts

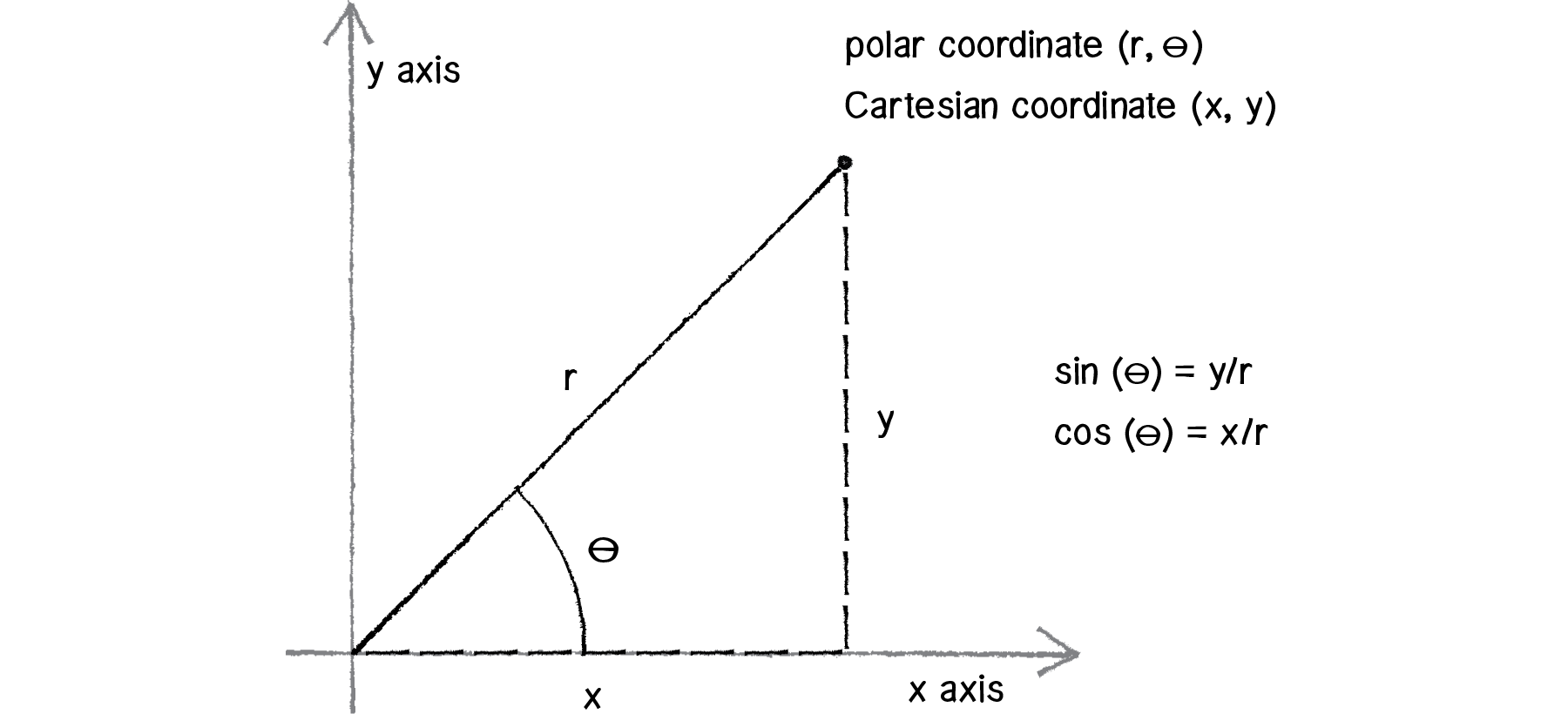
Our scientific toe and X squared plus y squared is going toe are square So the airport limit part and do 20 will become bad course square deter into our scientific data Divided by far put our is equal to zero I limit.

. Then the area enclosed by the polar curve is. In this section well look at the arc length of the curve given by r fleft theta righthspace05inalpha le theta le beta where we also assume that the curve is traced out exactly once. Called polar coordinates Polar Coordinates The rectangular coordinates xand ydescribe a point P in the plane as the intersection of two perpendicular lines.

In Maple you have to put square brackets around the curve and add the specification coordspolar. The 3d-polar coordinate can be written as r Φ θ. Cartesian to Polar Coordinates.

Here R distance of from the origin. Y r sin θ. We can define any conic in the polar coordinate system in terms of a fixed point the focus P rθ P r θ at the pole and a line the directrix which is perpendicular to the polar axis.

Using polar coordinates describe the level curves of the function defined by. Distance from the origin and two angles. R2 x2 y2 r x2y2 θ tan1 y x r 2 x 2 y 2 r x 2 y 2 θ tan 1 y x Lets work a quick example.

For a conic with eccentricity e e If 0 e 1 0 e 1 the conic is an ellipse. In the above graph angles are in radians where π radians 180. The first description is like giving x- and y-coordinates also known as Cartesian coordinates.

More precisely to describe a point in polar coordinates we describe how to get there from the origin by giving a direction and a distance r to go. Curves deﬁned using polar coordinates. We learned how to use the bounds of a double integral to describe a region in the plane using both rectangular and polar coordinates then later expanded to use the bounds of a triple integral to describe a region in space.

It is left as an exercise to use formula eqnpolarderiv and double-angle identities to show that. Using polar coordinates describe the level curves of the function defined byf x y 2 x y x 2 y 2 if x y 0 0 and f 0 0 0. 3d polar coordinates or spherical coordinates will have three parameters.

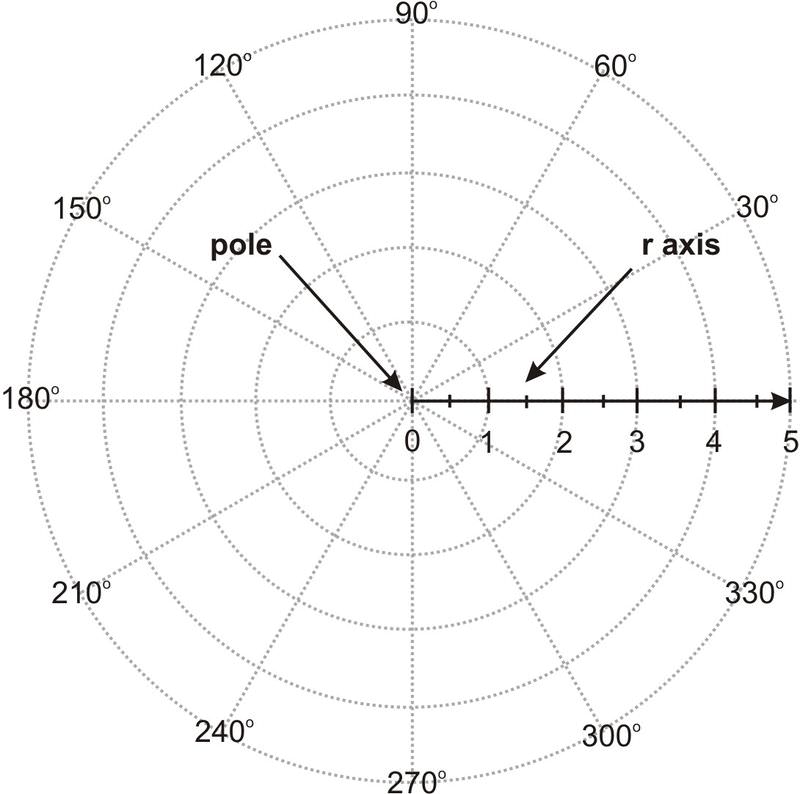
Radians Notice the curve is fully drawn once θ takes all values between 0 and 2 π. The line segment starting from the center of the graph going to the right called the positive x -axis in the Cartesian system is the polar axis. For a function z f x y.

The polar coordinate system. Polar coordinates describe a point P as the intersection of a circle and a ray from the center of that circle. Using polar coordinates describe the level curves of the function defined by.

Get solutions Get solutions Get solutions done loading Looking for the textbook. Then use that graph to trace out a rough graph in polar coordinates as in Figure figpolargraphb. Finding r and θ using x and y.

On the polar grid the equivalent of the positive x- axis on the rectangular grid. Use polar coordinates to solve int int_R ex2y2 dA. Example 1 Convert each of the following points into the given coordinate system.

Conversion from Polar to Rectangular Coordinates. Cartesian to Polar Conversion Formulas. Maple assumes that the first coordinate in the.

We can call the constant sin. A b Figure 911. 0 30 60 90 120 150 180 210 240 270 300 330 0 1 2 3.

2 α where 1 2. Find limit X comma by tending to the mobile as you well X squared by invite X squared. Solutions for Chapter 1610 Problem 9RE.

F x y 2 x y x 2 y 2 if x y 0 0 and f 0 0 0. Let r f θ rftheta r f θ be the equation of a polar curve and let θ α thetaalpha θ α and θ β thetabeta θ β be lines that bound an area enclosed by that polar curve. Find the vector and parametric equations for the line through.

When you use polar coordinates you are defining the points in terms of polar coordinates. They are de ned as follows. Using polar coordinates describe the level curves of the function defined by.

Use polar coordinates to help describe the level curves of. In this case sin. 2 θ c o n s t a n t.

To find the maxima minima and inflection points it is still necessary to find dydx and fracd2ydx2. Since r is a distance its always. Fx y 2xyx 2 y 2 if x y 0 and f0 0 0.

When you plot polar curves you are usually assuming that is a function of the angle and is the parameter that describes the curve. On the polar grid the coordinates of a point labeled where indicates the angle of rotation from the polar axis and represents the radius or the distance of the point from the pole in the direction of. The second is like giving polar coordinates.

When we say The storm is 10 miles northeast we are. Just as we did with the tangent lines in polar coordinates well first write the curve in terms of a set of parametric equations. Instead of using Cartesian xy coordinates we can describe points in the plane by specifying how far they are from some ﬁxed reference point thepole and the angle the line from the point to the pole makes with some reference direction.

X r cos θ. F x y 2xy x2 y2 hspace 02cmtext ifhspace 02cm xyneq 00 hspace 02cm text and hspace 02cm f 000 f xy 2xyx2 y2 if xy 00 and f 00 0. The convention is to treat the origin 00 as the pole and the reference direction as the positive.

Level Curves of Functions of Two Variables. The level curves of f are the curves f c o n s t a n t. D R 2 R the level curve of value c is the curve C in D R 2 on which f C c.

Graph of r 3 cos 2θ. To learn more see. R lies in the third quadrant and it bounded by the graphs of y x the y -axis and the circle x2.

For a general function z f x y slicing horizontally is a particularly important idea. Bless vice Quit using polar coordinates. Why is it Goto.

The center point is the pole or origin of the coordinate system and corresponds to The innermost circle shown in Figure contains all points a distance of 1 unit from. The area enclosed by a polar curve can be computed with integration.

Calculus Ii Polar Coordinates